Основное свойство дроби, в чем заключается, когда применяется, примеры

Сегодня мы поговорим, о том, в чем заключается основное свойство дроби, сформулируем и докажем его на конкретных примерах, рассмотрим практическое применение при решении задач.

Формулировка основного свойства дроби

Основное свойство дроби заключается в следующем:

Если числитель и знаменатель дроби умножить на одно и то же число — получится дробь, равная начальной.

В общем виде, основное свойство дроби выглядит следующим образом:

a ∙ m b ∙ m

a b

a : m b : m

a b

Наглядный пример

Возьмем дробь

1 2

и умножим её на 2.

Таким образом:

1 2

× 2 =

1 × 2 2 × 2

2 4

Исходя из основного свойства дроби:

1 2

2 4

Разберем наглядно это равенство. Для этого представим

1 2

2 4

в виде схематичных пицц.

Возьмем 2 пиццы, одну из которых разделим на 2 кусочка, а вторую на 4:

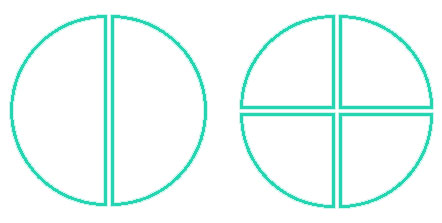
Теперь от первой возьмем один кусочек, а от второй — два:

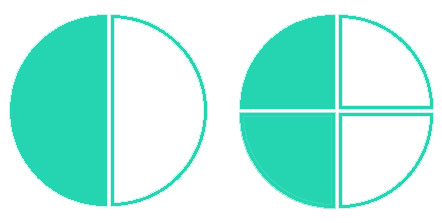
Первая пицца соответствет дроби

1 2

(т.е. один кусок из двух), а вторая дроби

2 4

(два куска из четырех). При этом наглядно можем убедиться, что в обоих случаях мы взяли одинаковое количество пиццы. Таким образом, несмотря на то, что одну разделили на 2 куска и взяли 1, а вторую разделили на 4 куска и взяли 2 — общее количество получилось одинаковым. Отсюда приходим к выводу, что основное свойство дроби — справедливо.

Когда применяется основное свойство дроби?

Основное свойство применяется, когда необходимо привести дробь к новому знаменателю (например, при решении арифметических задач) и при сокращении дробей.

Смотрите также:

Смотрите также
Калькуляторы
Последние примеры

Полезные материалы

Онлайн калькуляторы

Последние примеры

Оцените материал:

(Пока оценок нет)

Загрузка...

Основное свойство дроби