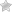Деление дробей 1(3/4) ÷ 1(1/8)

Подробное объяснение:

Деление смешанных дробей сводится в их преобразовании к неправильному виду, и умножению первой дроби на перевернутую вторую.

1. Приведём смешанные дроби к неправильному виду:
1

3 4

— смешанная дробь.

Для перевода в неправильную, необходимо целое число умножить на знаменатель и прибавить числитель, т.е.:

1
3 4
=
1 ∙ 4 + 3 4
=
7 4
1

1 8

— смешанная дробь.

Для перевода в неправильную, необходимо целое число умножить на знаменатель и прибавить числитель, т.е.:

1
1 8
=
1 ∙ 8 + 1 8
=
9 8
Переворачиваем вторую дробь:

7 4

÷

9 8

=

7 4

×

8 9

Перемножаем числители и знаменатели:

7 ∙ 8 4 ∙ 9
=
56 36
2. Сократим дробь:
В результате деления получилась дробь
56 36
, которую можно сократить.
Для этого необходимо найти наибольшее число, на которое делится и 56, и 36. В нашем случае это — 4. Разделим числитель и знаменатель на 4 и получим:
56 : 4 36 : 4
=
14 9
Подробнее о сокращении дробей, смотрите здесь.
3. Переведем неправильную дробь в смешанную:
14 9
— неправильная, т.к. числитель 14 больше знаменателя 9.
Переведем её в смешанную дробь. Для этого разделим числитель на знаменатель. Целая часть от деления — будет целой частью смешанной дроби, остаток от деления — числителем, знаменатель — останется прежним. В нашем случае это:
14 9
=
1
5 9
Подробнее о переводе в смешанную дробь, смотрите тут.